はんじょうのケーキ三等分問題（数学）

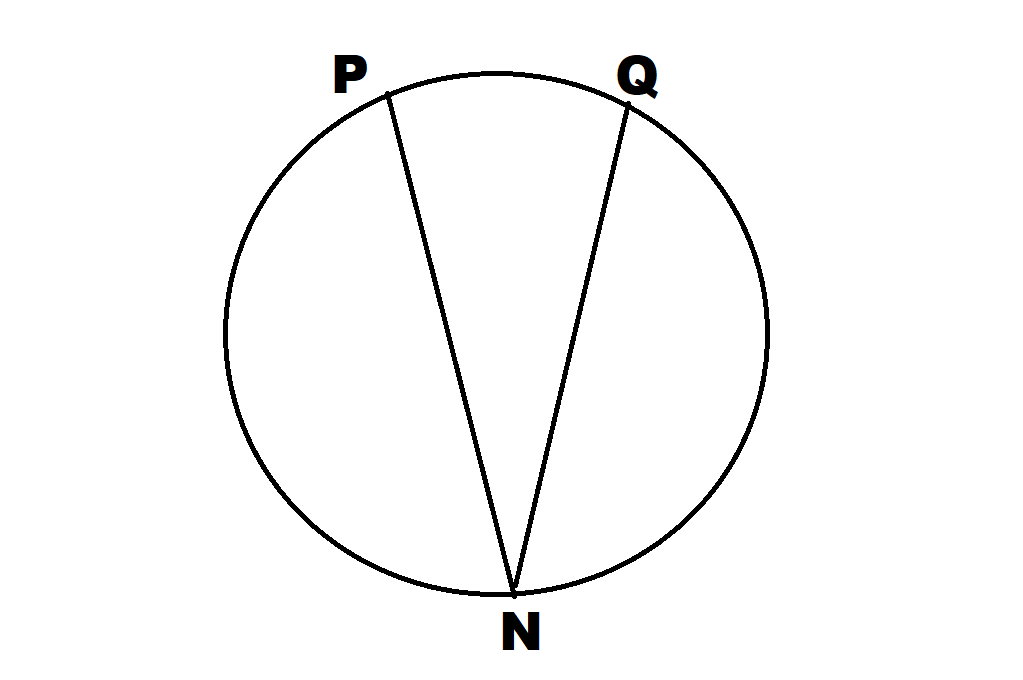
皆さんはゲーム実況者として活躍されている「はんじょう」という方をご存じでしょうか.彼はある日の配信でケーキを次のように三等分することを提案しました.

このように三等分するには,角 $PNQ$ を上手に定める必要があります.今回私はロープを使えばこの三等分が作図可能であることを証明しました.先行研究として数学ボーイZさんの「東大数学科院生がはんじょうさんによるケーキの $3$ 等分を解説します」という動画がYOUTUBEに上がっているのでそちらも参照してください.

角 $PNQ$ を $\theta$ として表し, $\theta$ が満足する等式を導きます.

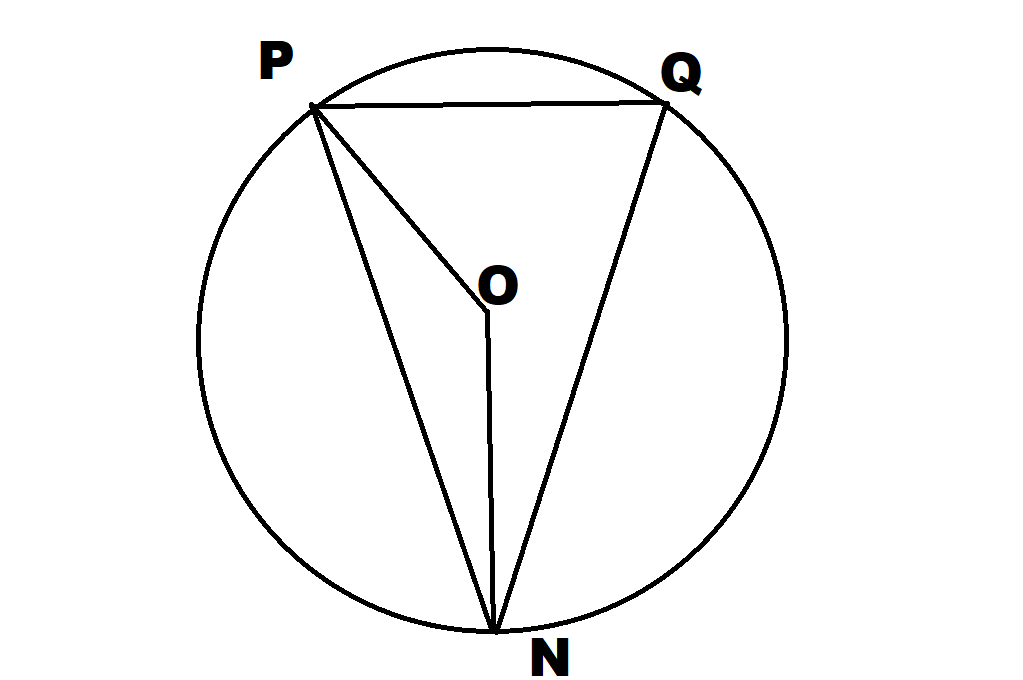
$O$ を円の中心とし円の半径を $1$ とします.ケーキを三等分することは,弦 $PN$ で切り取った部分の面積が $\dfrac{\pi}{3}$ であることを意味します.この部分は扇形 $PON$ から三角形 $PON$ を除いたものになります.よって扇形と三角形の面積を求めればよいことが分かります.

角 $PNO$ は $\dfrac{1}{2}\theta$ なので中心角 $PON$ は $\pi - \theta$ となります.よって扇形 $PON$ の面積は $\dfrac{\pi - \theta}{2}$ となります.

三角形 $PNO$ の面積は底辺が $2 \cos (\frac{\theta}{2} )$ で高さが $\sin ( \frac{\theta}{2})$ であるので, $\cos(\frac{\theta}{2})\sin(\frac{\theta}{2}) = \dfrac{1}{2} \sin (\theta)$ となります.

以上から切り取った部分の面積は $\dfrac{\pi - \theta}{2} - \dfrac{1}{2} \sin (\theta)$ となります.これが三等分 $\dfrac{\pi}{3}$ と等しいことから,等号で二つを結ぶことができて,整理すると角度 $\theta$ は
$\dfrac{1}{2}( \sin (\theta) + \theta) - \dfrac{\pi}{6} = 0$
を満たすことが分かりました.

さて弧 $PQ$ と弦 $PQ$ に注目します.中心角の定理から,角 $POQ$ は $2\theta$ となり,弧 $PQ$ と弦 $PQ$ の長さはそれぞれ $2\theta$ , $2\sin(\theta)$ となります.両者の和を取って, $\theta$ の関係式を使うと,弧 $PQ$ と弦 $PQ$ の長さの和は $\dfrac{2 \pi}{3}$ となります.これを用いて作図していきましょう.

円の中心 $O$ を作図することは既知とします.円にロープを巻き付け三等分すると,その長さは $\dfrac{2\pi}{3}$ になります.セロハンテープ等を使い,この長さの輪を作ります.輪の一部分を円周に沿わせていき,弦がピンと張るようにします.このときの輪の両端点を $P,Q$ とし,円弧 $PQ$ の中点を $M$ とします.中点は定規とコンパスでも作図可能です.

中点 $M$ と円の中心 $O$ を直線で結び,この直線と円が交わるもう一方の点を $N$ とします.このとき $PNQ$ はちょうどケーキを三等分します.(作図終わり)

コンパスと定規を用いた作図問題はよく知られていますが,そこにロープを加えるだけで面白い数学ができそうです.

名前のない定理

マニアックな数学

はんじょうのケーキ三等分問題（数学）