名前のない定理

マニアックな数学

はんじょうのケーキ三等分問題(数学)2

前回の記事
box-white.hatenablog.com
ではんじょうさんのケーキ三等分問題はロープを使えば解決できることを示しました.今回は別の方法でケーキを三等分することを考えます.

その前にはんじょうさんのようにケーキを三等分するときの角度を「はんじょう角」と呼ぶことにします.「はんじょう角」を $\theta$ とすると, $\sin (\theta) + \theta = \dfrac{\pi}{3}$ という性質がありました.

今回は次のように縦に三等分することを考えます.

hanjou2_1

hanjou2_2

このとき角 $AOB$ は「はんじょう角」に等しいことが示せます.

hanjou2_3

真ん中の部分の面積は三角形 $OBD$ と扇形 $OAB$ の和を二倍したものです.よって三角形 $OBD$ と扇形 $OAB$ の面積は $\dfrac{\pi}{6}$ となります.

角 $AOB$ を $\tau$ とします.扇形 $OAB$ の面積は $\dfrac{\tau}{2}$ です.三角形 $OBD$ の面積は $\sin\left( \dfrac{\tau}{2} \right) \cos \left( \dfrac{\tau}{2} \right)$ となります.これは $\dfrac{1}{2} \sin(\tau)$ と変形できます.よって角度 $\tau$ は式
$\dfrac{\tau}{2} + \dfrac{1}{2} \sin(\tau) = \dfrac{\pi}{6}$ を満たします.よって $\tau + \sin(\tau) = \dfrac{\pi}{3}$ となって $\tau$ が「はんじょう角」と等しいことが示せました.

最後に作図方法を考えてみましょう.前回の作図ができたものとして進めます.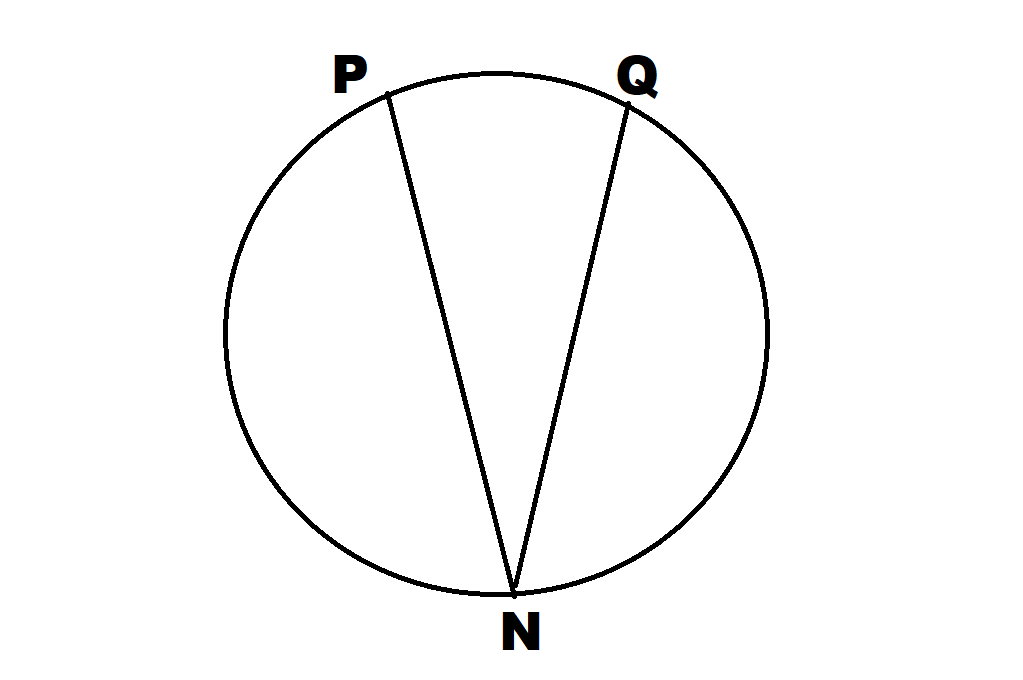

hanjou1

中心 $O$ から $NP$ と $NQ$ に平行な直線を引き,円との交点を求めます.

hanjou2_4

二つの交点を $A,B$ とします.

点 $A,B$ から $ON$ に平行な直線を書けば,ケーキを三等分できます.（ちょっと図が悪いのはご了承ください.）

「はんじょう角」にはこのような不思議な性質があることが分かりました.